Empirical Linear Regression Equation

Empirical linear regression equation. Empirical linear regression equation. Objective To establish a two-dimensional random variable (X, Y) Y dependency by X values. The correlation coefficient characteristics. Example Empirical Y linear regression equation with respect to X. Empirical covariance.

We bring out the equation that allows the calculation of the parameters a and b, when we know the average size.

1) , the value of absolute greatness closer to 1, the linear relationship between x y stronger..

2) If r> 0, then with increasing x, y - increases.

3) If r <0, then with increasing x, y - decreasing.

4) r is independent of x and y of the graduated scale. For example all xi multiplied in 1000, the correlation coefficient does not change.

Since the covariance, correlation coefficient of the regression equation find the need to calculate averages.

The drawings are postponing (x, y) in a two-dimensional random size and the regression line.

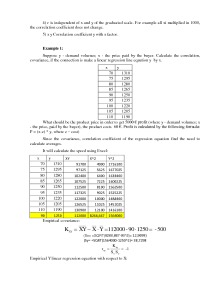
The company wants to install a legal relationship between the number of sellers and sales volume as measured in tonnes per month.

Calculated covariance, correlation coefficient. Develop regression equation and put the drawing.

Since the covariance, correlation coefficient of the regression equation, can be found by calculating averages.

The drawings are postponing (x, y) in a two-dimensional random size and the regression line. Regression line points: